Searle's Chinese Room —Revealed
Turing machine theory explains both formal symbol manipulation and the systems reply—precisely.
Philosopher John Searle's famous Chinese room argument (CRA) contends that regardless of a computer's observable inputs and outputs, no type of program could by itself enable a computer to think internally like a human. The reason is as follows. Internally, a computer uses its given program rules to syntactically manipulate its symbols purely formally (by their shapes alone). It never subjectively associates its symbols with any semantic content lying beyond the symbols' formal identities. In contrast, the ability to interpret symbols into subjective meanings is a clear hallmark of human thought. Thus, if human thought were just computation, we would understand nothing internally because inside computers it is always 100% syntax, 0% semantics.
Philosophy or Mathematics?
As a philosophical argument, the CRA has stood the test of time, enticing novice and expert alike for over 4 decades. It is popular because it blends a familiar view of computers with an intuitive story for why they can't match us. However, unlike many philosophical arguments, the CRA has a mathematical basis: the theory of computation. Under the bright lights of the theory, the CRA does not stand up so well. The theory clearly explains both Searle's intuitions and the CRA's undeniable flaws.
Computers Understand English?!
If computers lack semantics, then why must the Searle-computer's programs be in English?
For example, the theory highlights this telling discrepancy in Searle's argument. If computers lack semantics, then why must the Searle-computer's programs be in English? If computers are purely formal symbol manipulators, without one iota of intentionality regarding the symbols they receive, then why not allow the programs to be written in, say, Chinese, binary, or Martian? Under Searle's own analysis, the semantics of English should be irrelevant to the Searle-computer, right?
Of course, the use of English in programs does matter to the Searle-computer—quite a lot! The theory of computation explains this discrepancy precisely. Spoiler alert: The CRA's linchpin: formal symbol manipulation, is merely a special case.
Two Inputs, Two Dispositions, and...
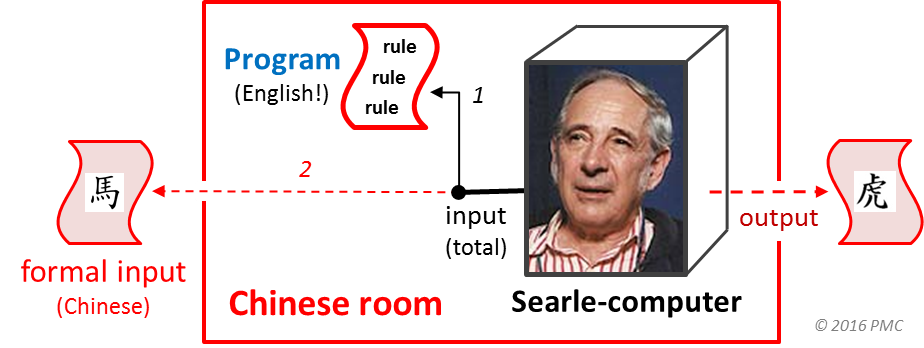
The Searle-computer in fact has two kinds of inputs: (1) the English program found inside the room and (2) the Chinese from the outside. And the Searle-computer has two completely different dispositions toward each kind. As we well know, it processes the Chinese symbols purely formally, syntactically, with no inkling of their meanings. Fine. We've got that.
Now Searle would like the story to end there. But the nagging question of the English program input remains. To function properly, the Searle-computer must correctly interpret those program rules with all the intentionality it can muster! In other words, the Searle-computer must somehow causally connect the programs' symbols with the physical entities and processes that they represent—a non-formal transformation that realizes symbolic representations as specific real events. For some reason, we don't hear about this topic from Searle the philosopher.
Fortunately, everyone can learn the explanation for themselves, courtesy of Alan Turing, the mathematician.
Two Computations: The Systems Reply —Explained
The theory of computation explains both formal symbol manipulation and the systems reply—precisely. A full understanding of the CRA entails three concepts and their relationships:
- Turing machines,
- programs, and
- universal Turing machines.
2016: How Long Can the Angels Keep Dancing in the Chinese Room? 1993: Turing Machines and Semantic Symbol Processing: Why Real Computers Don’t Mind Chinese Emperors
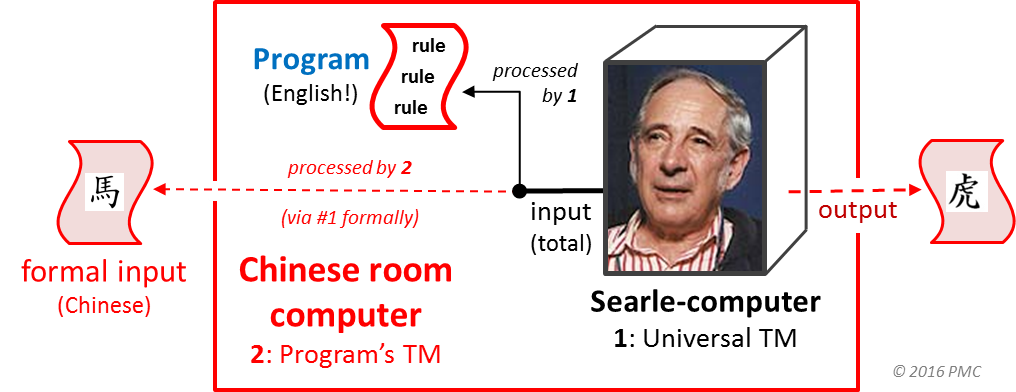
In a nutshell, Turing machines (TMs) are general computers of all types. Programs are "TM blueprints", each of which describes the structure and functioning of a type of TM. And universal Turing machines (UTMs) are just the highly specialized subclass of fully programmable TMs. Unlike general TMs, UTMs must always faithfully execute the programs of all TM types. Hence, UTMs can never process their all of their input completely "of their own accord", unlike TMs in general.
Turing Machine
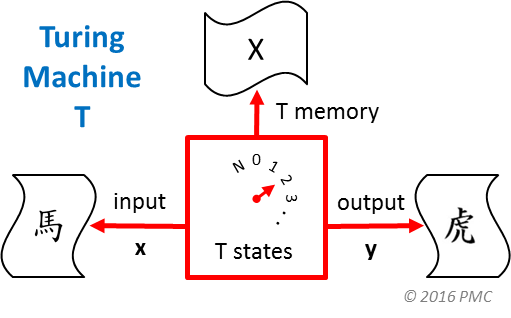
The Turing machine model of computation is a mathematical construct that describes the abstract structure and functioning of all types of "computers".
A TM, T, has a set of internal states, which partially determine its actions. T also has a tape (shown here in three parts), which contains T's (1) inputs, (2) internal memory, and (3) outputs. Step by step, a machine T executes its computation by using the content of its inputs, internal states, and memory to ultimately produce its outputs. A key characteristic of every TM is that its structure and function (its set of different steps) is finite, which means that it can be specified completely.
Program
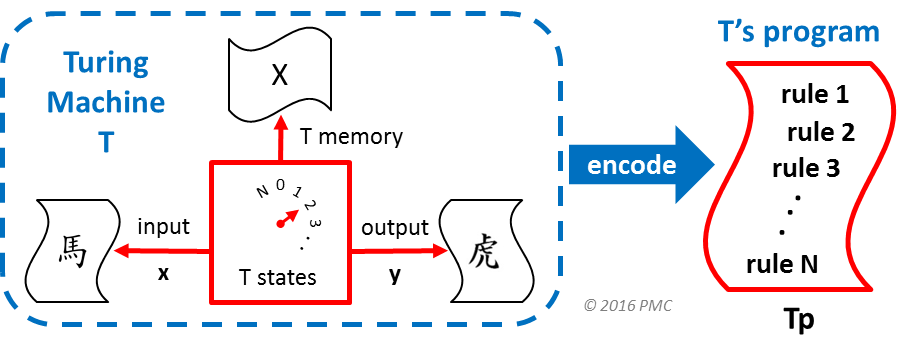
Every program is the encoded form of a TM of some type.
A program Tp specifies structure and functioning of a TM T, including the "rules" that govern each step of T's execution. Thus, a program is like a "blueprint" that one can use to build and run TM instances of the specified type.
Universal Turing Machine
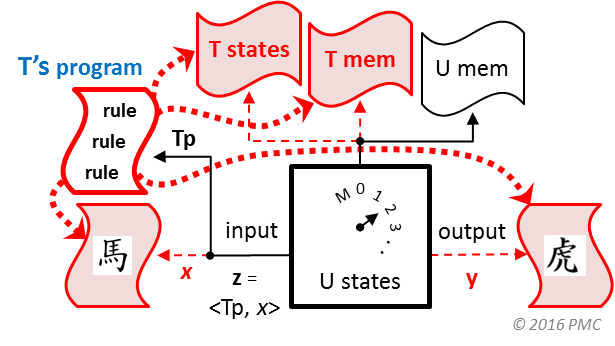
A universal Turing machine is a very special type of TM that can instantiate any type of TM via its program. It is thus the mathematical model of a "(fully) programmable computer".
Every UTM, U, has an input, z, that has two parts: (1) a program, Tp, specifying some type of TM, and (2) a "formal" input, x.
When U runs, it uses program input Tp to instantiate TM computation T, which then processes input, x.
Thus, a UTM always entails two TM computations:
Everyone is entitled to his own opinion, but not to his own facts. — Daniel Patrick Moynihan
The Chinese Room Argument vs. Turing Machines
The theory of computation for Turing machines explains precisely and objectively why the systems reply refutation of the Chinese room argument is at least "half correct": there is irrefutably a second significant computation in the room, which is distinct from Searle's own universal (UTM) one, the only one that he can consciously introspect.
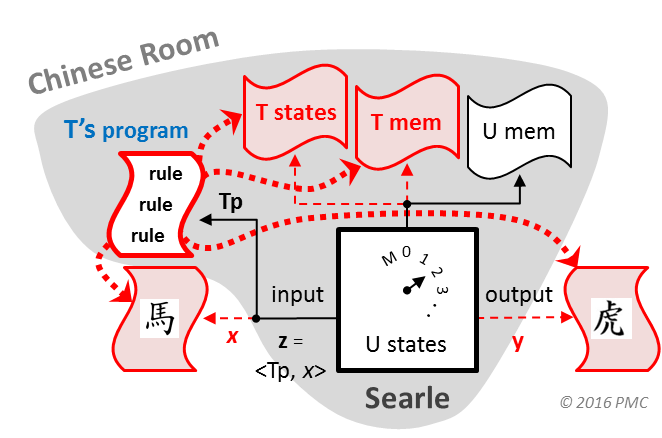
The CRA is indeterminate because Searle only shows that his own universal computation, U, is guilty of purely formal symbol manipulation (pure syntax) regarding the Chinese inputs, x. Such formal processing of nominal inputs is a special artifact of UTMs, which derives from being strictly governed by an external program, Tp. But it is not an inherent characteristic of all TMs. Indeed, it is not even true of UTMs themselves regarding their program inputs.
The second computation—that of machine T via program Tp—is the only computation that is directly responsible for processing the Chinese from input to output. And for all we know, it might be processing and understanding the Chinese inputs like a human Chinese speaker would. However, the theory of computation does not entail the Turing Test, so it does not sanction the further conclusion that Chinese is definitely being understood in human fashion (as opposed to some other kind of process, e.g., statistical, etc.).
Because we never learn how TM-computer T actually processes the Chinese, the CRA proves absolutely nothing about "Strong AI" or computationalism.
Q.E.D.